In [1]:
import dependencies
import copy
import numpy as np
from IPython.display import display, HTML
from hvac.heat_loss_calc import BuildingElement, BuildingCompositeElement, BuildingPart, Space
from hvac.components import Radiator, ControlValve, ControlValveMotor
from hvac.process import Room, OutsideTemperature, DeadTime
from hvac.controller import OnOffController, DataLogger, OutdoorResetController
from nummath import graphing

RUIMTEVERWARMING: DYNAMISCHE SIMULATIE MET AAN/UIT-REGELING

In deze Jupyter Notebook wordt een computerprogramma gedemonstreerd waarmee de temperatuurregeling in verwarmingsbedrijf van een fictieve ruimte dynamisch wordt gesimuleerd. De ruimte wordt verwarmd d.m.v. een radiator. De regelaar is een aan/uit-regelaar waarmee het volumedebiet (Vw) verwarmingswater, dat naar de radiator stroomt, wordt gecorrigeerd afhankelijk van de gemeten ruimtetemperatuur (Tr). Het corrigerend orgaan is een regelklep in het radiatorcircuit. Naast de aan/uit-regelaar kan er ook nog een wateraanvoertemperatuuregelaar (stookregelaar) worden toegepast die de aanvoertemperatuur van het verwarmingswater (Twe) naar de radiator regelt afhankelijk van de gemeten buitentemperatuur (To). De wateraanvoertemperatuurregelaar kan ingrijpen op de brander van de verwarmingsketel of op een mengklep aan het begin van de radiatorcircuits.

De regelkring kan in een blokschema schematisch worden voorgesteld. De drie hoofdblokken in het schema zijn: de regelaar, de regelklep (het "corrigerend orgaan") en het proces. De regelaar krijgt via meting informatie over de momentane waarde van de procesgrootheid, in casu de (lucht)temperatuur in de ruimte (Tr). Op basis van de deviatie tussen de gemeten en de gewenste waarde van de procesgrootheid (e) bepaalt de regelaar het regelcommando (hier: ofwel "aan" of 100%, ofwel "uit" of 0%). Het regelcommando (OUT) wordt aan de regelklep toegevoerd en stemt overeen met de klepstand (h) die de regelklep moet innemen (hier: ofwel volledig open, ofwel volledig dicht). Daarmee wordt het volumedebiet verwarmingswater (Vw) gewijzigd dat naar de radiator in de ruimte stroomt. De warmteafgifte van een radiator (Qe) wordt immers o.a. beïnvloed door het volumedebiet van het verwarmingswater dat door de radiator stroomt; de twee andere invloedsfactoren zijn de aanvoertemperatuur van het verwarmingswater (Twe) en de ruimtetemperatuur (Tr).

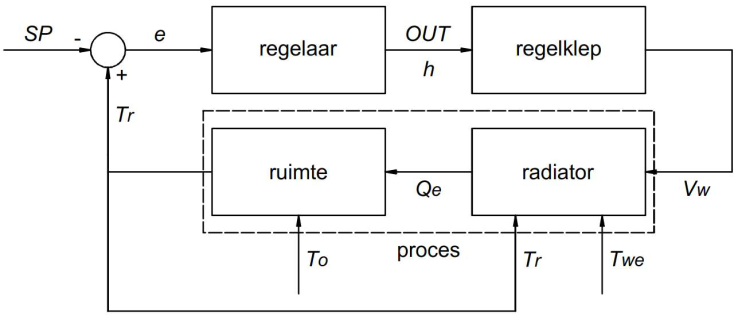
Onder paragraaf 1 wordt de opmaak van het procesmodel in het computerprogramma beschreven. Het proces omvat de radiator en de ruimte waarin de radiator zich bevindt. Voor de computersimulatie moet de ruimte door een wiskundig model worden voorgesteld. In casu is een sterk vereenvoudigd model toegepast. Een ruimte wordt voorgesteld door een lineair thermisch netwerk samengesteld uit twee temperatuurknopen (een 2de orde systeem), nl. het luchtvolume van de ruimte en de bouwschil die de ruimte omhult. In deze demonstratie is bovendien gemakshalve een homogene bouwschil verondersteld, die slechts uit één bouwdeel bestaat. Vandaar de vermelding hierboven dat het om een fictieve ruimte gaat.

In paragraaf 2 wordt het model van de regelklep beschreven. De regeklep bestaat in feite uit twee te onderscheiden onderdelen: de regeklepmotor en de eigenlijke tweewegregelklep.

In paragraaf 3 wordt het model van de aan/uit-regelaar en de wateraanvoertemperatuurregelaar beschreven. Noteer dat de wateraanvoertemperatuurregelaar hier ook geïdealiseerd is voorgesteld: de aanpassing van de wateraanvoertemperatuur volgt via de regelaarkarakteristiek (stookcurve) ogenblikkelijk de verandering van de buitentemperatuur. In realiteit vergt de aanpassing van de wateraanvoertemperatuur volgend op een verandering van de buitentemperatuur tijd.

In paragraaf 4 wordt een datalogger aangemaakt. In realiteit zal deze niet in de regelkring voorkomen. Het betreft een "helper-object" van het computerprogramma dat zal dienen om de ogenblikkelijke parameterwaarden van de gesimuleerde regelkring op te slaan, zodat na het doorlopen van de simulatieberekeningen, de parameterwaarden in een grafiek langs de tijdsas kunnen uitgezet worden.

In paragraaf 5 wordt de volledige regelkring in het programma geconfigureerd, waarna de simulatieberekeningen van de regelkring worden uitgevoerd (par. 5.5).

In paragraaf 6 worden, nadat de simulatieberekeningen zijn voltooid, de berekeningsresultaten in drie grafieken voorgesteld (grafiek 1: verloop temperaturen in de tijd, grafiek 2: warmteafgifte van de radiator in de loop van de tijd en grafiek 3: regelcommando + klepstand in de loop van de tijd).

1. Opmaak van het wiskundig simulatiemodel van de verwarmde ruimte

1.1 Configuratie van de bouwdelen die de ruimte begrenzen

Hieronder wordt de samenstelling van een buitenmuur gedefinieerd. Deze buitenmuur is samengesteld uit:

  • een buitenblad samengesteld uit gevelbaksteen (b x h x d = 188 x 65 x 88 mm) en cementvoeg (12 mm)
  • een matig verluchte luchtspouw (20 mm)
  • een isolatielaag (60 mm)
  • een binnenblad samengesteld uit snelbouwbaksteen (b x h x d = 288 x 138 x 138 mm) en cementvoeg (12 mm)
  • een pleisterlaag (10 mm)

Buitenblad

In [2]:
brick_ext = BuildingElement(
    A=188.0e-3 * 65.0e-3,  # oppervlakte van 1 baksteen
    t=88.0e-3,             # dikte van 1 baksteen
    k=0.91,                # warmtegeleidingscoëfficiënt van de baksteen
    rho=1500.0,            # massadichtheid van de baksteen
    cm=840.0               # specifieke warmtecapaciteit van de baksteen
)

joint_ext = BuildingElement(
    # oppervlakte van de cementvoeg rond 1 baksteen (1 langse voeg + 1 kopse voeg)
    A=12.0e-3 * (188.0e-3 + 12.0e-3) + 12.0e-3 * 65.0e-3,
    t=88.0e-3, 
    k=1.5, 
    rho=1800.0, 
    cm=840.0
)

# De baksteen en omringende cementvoeg vormen gecombineerd het buitenblad van de buitenmuur.
leaf_ext = BuildingCompositeElement(brick_ext, joint_ext)
leaf_ext.num_of_layers = 4

Luchtspouw

In [3]:
air_cavity = BuildingElement(
    t=20.0e-3, 
    r=0.085,    # specifieke warmteweerstand van de luchtspouw
    rho=1.205,  # massadichtheid lucht
    cm=1005.0   # specifieke warmtecapaciteit van lucht
)
air_cavity.num_of_layers = 1

Isolatielaag

In [4]:
insulation = BuildingElement(
    t=60.0e-3, 
    k=0.041, 
    rho=25.0, 
    cm=840.0, 
    corr_r=-0.1  # correctiefactor voor de plaatsing van de isolatie
)
insulation.num_of_layers = 3

Binnenblad

In [5]:
brick_int = BuildingElement(
    A=288.0e-3 * 138.0e-3, 
    t=138.0e-3, 
    k=0.32, 
    rho=1100.0, 
    cm=840.0
)

joint_int = BuildingElement(
    A=12.0e-3 * (288.0e-3 + 12.0e-3) + 12.0e-3 * 138.0e-3, 
    t=138.0e-3, 
    k=1.0, 
    rho=1900.0, 
    cm=840.0
)

leaf_int = BuildingCompositeElement(brick_int, joint_int)
leaf_int.num_of_layers = 6

Pleisterlaag

In [6]:
stucco = BuildingElement(
    t=10.0e-3, 
    k=0.57, 
    rho=1300.0, 
    cm=840.0
)
stucco.num_of_layers = 1

Compleet samengestelde buitenmuur

In [7]:
wall = BuildingPart(leaf_ext, air_cavity, insulation, leaf_int, stucco, r_conv_in=0.13, r_conv_out=0.04)
wall.calculate_effective_capacity()

Noot
r_conv_in is de specifieke convectieweerstand aan de binnenzijde (geklimatiseerde zijde) van het bouwdeel, r_conv_out is de specifieke convectieweerstand aan de buitenzijde van het bouwdeel.

1.2 Configuratie van de ruimte

Voor de eenvoud zullen we aannemen dat de ruimte wordt omgeven door een homogene bouwschil (alle bouwdelen die de ruimte omgeven zijn identiek samengesteld). Uiteraard is dit geen realistisch gegeven. Deuren, ramen, plafond, vloer kunnen op analoge wijze worden gedefinieerd zoals de muur hierboven onder par. 1.1.

De binnenafmetingen van de ruimte zijn:

  • lengte 6 m
  • breedte 4 m
  • hoogte 2,7 m

De bouwschil is 30 cm dik.

De ruimte heeft 4 muren, een vloer en plafond:

In [8]:
walls = [copy.deepcopy(wall) for _ in range(4)]
floor = copy.deepcopy(wall)
ceiling = copy.deepcopy(wall)

De voor- en achtermuur en de twee zijmuren hebben dezelfde afmetingen. We bepalen de binnen- en buitenoppervlakte van de muren met de opgegeven afmetingen.

In [9]:
# front and back wall have indices 0 and 1
for i in range(2):
    walls[i].set_areas(
        A_inside=6.0 * 2.7,
        A_outside=(6.0 + 2 * 0.3) * 2.7
    )

# the two side walls have indices 2 and 3
for i in range(2, 4):
    walls[i].set_areas(
        A_inside=4.0 * 2.7,
        A_outside=(4.0 + 2 * 0.3) * 2.7
    )

Binnen- en buitenoppervlakte van de vloer:

In [10]:
floor.set_areas(
    A_inside=6.0 * 4.0,
    A_outside=(6.0 + 2 * 0.3) * (4.0 + 2 * 0.3)
)

Binnen- en buitenoppervlakte van het plafond:

In [11]:
ceiling.set_areas(
    A_inside=6.0 * 4.0,
    A_outside=(6.0 + 2 * 0.3) * (4.0 + 2 * 0.3)
)

De ruimte kan nu gedefinieerd worden:

In [12]:
room = Space()
room.set_dimensions(length=6.0, width=4.0, height=2.7)
room.set_building_parts(*walls, ceiling, floor)

1.3 Ontwerpcondities vastleggen

De ontwerptemperaturen aan de binnen- en buitenzijde van de bouwdelen en binnenin en buiten de ruimte worden vastgelegd. De temperatuur aan de buitenzijde van een bouwdeel is niet noodzakelijk gelijk aan de buitentemperatuur (de temperatuur van de buitenomgeving). Een ruimte kan grenzen aan een aanpalende ruimte waarvan de binnentemperatuur dan gelijk is aan de temperatuur aan de buitenzijde van het beschouwde bouwdeel. Het warmteverlies van de ruimte wordt berekend door achtereenvolgens het warmteverlies door elk bouwdeel die de ruimte omgeeft te berekenen en deze warmteverliezen dan op te tellen. Om de thermische weerstand van de omhullende bouwschil van de ruimte te berekenen wordt het temperatuurverschil tussen de binnentemperatuur van de ruimte en de buitentemperatuur gedeeld door het totaal warmteverlies van de ruimte. Bijgevolg, het is alsof we de afzonderlijke ruimte naar de buitenomgeving brengen, maar ervoor zorgen dat het totale warmteverlies van de ruimte daarbij ongewijzigd blijft. De berekende thermische weerstand van de ruimte is m.a.w. gerefereerd aan de temperatuur van de buitenomgeving.

In [13]:
T_in_des = 22.0  # °C
T_out_des = -10.0  # °C
In [14]:
for bp in room.building_parts:
    bp.set_temperatures(T_inside=T_in_des, T_outside=T_out_des)

room.set_temperatures(T_inside=T_in_des, T_outside=T_out_des)

1.4 Warmteverlies onder ontwerpcondities, thermische weerstand en capaciteit van de ruimte berekenen

Nu de ruimte volledig is geconfigureerd, kan het warmteverlies berekend worden. Tevens worden de globale transmissieweerstand van de bouwschil, de statische en effectieve thermische capaciteit van de bouwschil en de statische thermische capaciteit van het luchtvolume in de ruimte berekend. Het onderscheid tussen de statische en effectieve thermische capaciteit van de bouwschil is essentieel. In werkelijkheid zullen in de bouwschil temperatuurgradiënten in alle richtingen voorkomen. Om de bouwschil realistisch te modelleren, dienen in principe alle verschillende bouwdelen die de bouwschil samenstellen, door complexe, intergeconnecteerde thermische netwerken worden voorgesteld. In ons vereenvoudigd wiskundig model wordt de bouwschil echter maar door één temperatuurknoop voorgesteld. Zou men daaraan de statische thermische capaciteit koppelen, dan zou dit betekenen dat verondersteld wordt dat de bouwschil slechts één uniforme temperatuur bezit (m.a.w. uniform wordt opgewarmd of afgekoeld). De toepassing van de effectieve capaciteit laat toe om de bouwschil bij benadering toch als één temperatuurknoop te blijven opvatten. De effectieve capaciteit van een bouwdeel wordt bepaald door een multiknopig lineair thermisch netwerk van het bouwdeel uit te rekenen en vervolgens een evenwaardig of equivalent éénknopig model te bepalen dat voor dezelfde amplitude van de buitentemperatuur dezelfde amplitude van de warmtestroom aan de binnenzijde van het bouwdeel oplevert als in het multiknopig lineair thermisch netwerk. De bepaling van de effectieve thermische capaciteit wordt gedemonstreerd in de Jupyter Notebook Effectieve thermische capaciteit van een buitenmuur.

In [15]:
room.calculate()
heat_loss_calculation = room.get_results()

display(HTML(
    "<ul>"
    f"<li>Warmteverlies door transmissie onder ontwerpcondities = <b>{heat_loss_calculation['Q_tr']:.3f}</b> W</li>"
    f"<li>Thermische weerstand van de bouwschil = <b>{heat_loss_calculation['R_tr']:.3f}</b> K/W</li>"
    f"<li>Thermische capacititeit van het luchtvolume in de ruimte = <b>{heat_loss_calculation['C_ra']:.3e}</b> J/K</li>"
    f"<li>Statische thermische capaciteit van de bouwschil = <b>{heat_loss_calculation['C_bm_stat']:.3e}</b> J/K</li>"
    f"<li>Effectieve thermische capaciteit van de bouwschil = <b>{heat_loss_calculation['C_bm_eff']:.3e}</b> J/K</li>"
    "</ul>"
))
  • Warmteverlies door transmissie onder ontwerpcondities = 1727.938 W
  • Thermische weerstand van de bouwschil = 0.019 K/W
  • Thermische capacititeit van het luchtvolume in de ruimte = 7.847e+04 J/K
  • Statische thermische capaciteit van de bouwschil = 2.969e+07 J/K
  • Effectieve thermische capaciteit van de bouwschil = 1.862e+06 J/K

1.5 Radiator selecteren

Nadat de warmteverliesberekening is voltooid (paragrafen 1.1 t.e.m. 1.4), kennen we de thermische karakteristieken van de ruimte die we nu kunnen gebruiken om de temperatuurregeling van de ruimte te simuleren. De ruimte, inclusief de radiator(en) in de ruimte, vormen het regelproces. Het regelproces wordt door een afzonderlijk object van de klasse Room gemodelleerd (en is niet te verwarren met het object van de klasse Space die uitsluitend voor de warmteverliesberekening en de bepaling van de thermische karakteristieken van een ruimte dient).

Eerst zullen we een radiator selecteren om in de ruimte te plaatsen.

Selectie van de radiator
We kiezen een radiator die onder nominale condities een warmtevermogen afgeeft die in de lijn ligt van het berekende warmteverlies.

In [16]:
radiator = Radiator(
    Qe_nom=1886.0,         # nominaal warmtevermogen [W] 
    Twe_nom=75.0,          # nom. wateraanvoertemperatuur [°C]
    Twl_nom=65.0,          # nom. waterretourtemperatuur [°C]
    Tr_nom=20.0,           # nom. ruimtetemperatuur [°C]
    n=1.3279               # radiatorexponent
)

Keuze wateraanvoertemperatuur en berekening van het vereist volumedebiet verwarmingswater door de radiatoren onder ontwerpcondities
We houden de opgegeven, nominale wateraanvoertemperatuur aan. De gewenste ruimtetemperatuur werd reeds vastgelegd in de warmteverliesberekening van de ruimte (zie par. 1.3). Het warmteverlies onder ontwerpcondities is eveneens berekend (zie par. 1.4).

In [17]:
# vereist volumedebiet verwarmingswater onder ontwerpcondities [m^3/s]
Vw_max = radiator.calc_Vw(
    Qe=heat_loss_calculation['Q_tr'], 
    Twe=radiator.nominal_specs['Twe'],  # wateraanvoertemperatuur naar de radiator [°C] 
    Tr=T_in_des
) 

display(HTML(f"Maximum volumedebiet verwarmingswater (volumedebiet onder ontwerpcondities) = <b>{Vw_max * 1000.0 * 60.0:.3f}</b> L/min"))
Maximum volumedebiet verwarmingswater (volumedebiet onder ontwerpcondities) = 2.052 L/min

1.6 Aanmaken van het ruimtemodel

Alle informatie om het ruimtemodel aan te maken en te initialiseren is nu voorhanden. We dienen alleen nog een tijdstap in te stellen waarmee de numerieke berekeningen zullen uitgevoerd worden.

Tijdstap van de simulatieberekeningen

In [18]:
dt = 60.0  # seconden

Ruimtemodel
Voor de thermische massa C_bm van de bouwschil maken we gebruik van de effectieve thermische capaciteit.

In [19]:
room = Room(
    R_tr=heat_loss_calculation['R_tr'],
    C_ra=heat_loss_calculation['C_ra'],
    C_bm=heat_loss_calculation['C_bm_eff'],
    dt=dt,
    radiator=radiator
)

2. Configuratie van de regelklep

De regelklep omvat de regelklepmotor en de eigenlijke regelklep. De regelklepmotor ontvangt van de regelaar een regelcommando dat inhoudt naar welke klepstand de klepmotor de klepsteel van de regelklep moet bewegen. Het regelcommando kan een waarde zijn tussen 0% en 100% (klep volledig dicht c.q. klep volledig open).

Regelklepmotor
De regelklepmotor wordt gekenmerkt door de snelheid waarmee de klepmotor de klepsteel doet bewegen. De snelheid wordt uitgedrukt in procenten van de klepsteelweg per seconde. Bv. 5% / seconde betekent dat de klepsteel in één seconde 5% van de totale weg aflegt. De berekeningen worden in tijdstapjes uitgevoerd. De maximale weg die de klepsteel kan afleggen in één tijdstap dt wordt bepaald door het produkt van de ingestelde snelheid en de grootte van de tijdstap. Indien de gevraagde klepverplaatsing in een tijdstap groter is dan de maximale weg, wordt de klepverplaatsing begrensd tot deze waarde. Dit impliceert dat de klepstand die de regelklep inneemt in een tijdstap niet per se zal overeenstemmen met de klepstand die de regelaar vraagt.

In [20]:
valve_motor = ControlValveMotor(travel_speed=0.5, dt=dt)

Regelklep
De regelklep is standaard van het equiprocentuele type. De regelklep ontvangt de gevraagde kleppositie van de klepmotor. M.b.v. de klepautoriteit a en het regelbereik Rvan de geïnstalleerde regeklep kan de effectieve klepkarakteristiek van de regelklep worden berekend. Daaruit volgt voor een gegeven kleppositie (in procenten) een zeker volumedebiet uitgedrukt in procenten van het volumedebiet dat de regelklep in volledig geopende stand zal doorlaten. Om de absolute waarde van dit volumedebiet te kunnen bepalen bij een zekere kleppositie, moet het programma weten welke het maximaal volumedebiet Vmaxzal zijn dat doorgelaten wordt wanneer de klep volledig openstaat. Dit maximumdebiet werd hierboven bepaald in par. 1.5.

In [21]:
control_valve = ControlValve(
    a=0.5,           # klepautoriteit van de geïnstalleerde regelklep
    R=150.0,         # inherent regelbereik van de regelklep
    V_max=Vw_max,    # maximum debiet dat de regelklep in volledig geopende stand doorlaat 
)                    # (= vereist volumedebiet onder ontwerpcondities) [m^3/s]

3. Configuratie van de regelaars

3.1 De aan/uit-regelaar

We zullen de temperatuur in de ruimte regelen met een aan/uit-regelaar. De parameters van een aan/uit-regelaar zijn:

  • Het setpunt SP, d.i. de gewenste ruimtetemperatuur waarnaar de regelaar de ruimtetemperatuur moet regelen (in casu de ontwerp-binnentemperatuur)
  • De bovengrens HL_offset die de bovenste limiet van de schakeldifferentie vastlegt t.o.v. het setpunt waarbinnen de regelaar met aan- en uitschakelen de ruimtetemperatuur regelt.
  • De ondergrens LL_offset die de onderste limiet van de schakeldifferentie vastlegt t.o.v. het setpunt.
  • Het meetbereik PV_range waartussen de regelaar de procesgrootheid (temperatuur) kan meten.
  • De bemonsteringstijd dt van de regelaar (in seconden); d.i het tijdsverloop tussen 2 opeenvolgende metingen (in casu is de bemonsteringstijd gelijk aan de tijdstap van de simulatieberekeningen).
  • De regelrichting ctrl_dir van de regelaar: direct werkend (1) of indirect werkend (-1)
In [22]:
on_off_controller = OnOffController(
    SP=T_in_des,                  
    HL_offset=1.0,                
    LL_offset=-1.0,               
    PV_range=(-100.0, 100.0),     
    dt=dt,                        
    ctrl_dir=-1                   
)

3.2 De wateraanvoertemperatuurregelaar

Een wateraanvoertemperatuurregelaar regelt de wateraanvoertemperatuur naar de radiator i.f.v. de buitentemperatuur (outdoor reset control). Met de ingestelde regelkarakteristiek (reset line) bepaalt de regelaar de wateraanvoertemperatuur die hoort bij de gemeten buitentemperatuur. De regelkarakteristiek is een rechte met 2 coëfficiënten: T_we = c0 + c1 * T_out. De 2 coëfficiënten kunnen, ofwel extern berekend worden en rechtstreeks aan de OutdoorResetController worden doorgegeven, ofwel door de OutdoorResetController worden berekend (met de functie calc_reset_line). Om de regelkarakteristiek te kunnen berekenen, moeten volgende parameters ingegeven worden:

  • de ontwerpbelasting van de ruimte [W]
  • de ontwerpbuitentemperatuur [°C]
  • de wateraanvoertemperatuur onder ontwerpcondities [°C]
  • de ontwerpbinnentemperatuur [°C]
  • de radiator in de ruimte (Radiator-object)
In [23]:
outdoor_reset_controller = OutdoorResetController()
outdoor_reset_controller.calc_reset_line(
    Q_load_des=heat_loss_calculation['Q_tr'],
    T_out_des=T_out_des,
    T_we_des=room.radiator.nominal_specs['Twe'],
    T_in_des=T_in_des,
    radiator=radiator
)
In [24]:
c0, c1 = outdoor_reset_controller.get_coefficients()
display(HTML(
    f"Vergelijking van de regelaarkarakteristiek: <code>T_we = <b>{c0:.3f}</b> + <b>{c1:.3f}</b> * T_out</code>"
))
Vergelijking van de regelaarkarakteristiek: T_we = 61.116 + -1.568 * T_out
In [25]:
graph = outdoor_reset_controller.plot_reset_line(fig_size=[8, 8], dpi=96)
graph.show_graph()

4. Configuratie van een datalogger

De datalogger is een object die de waarden van de diverse parameters in de regelkring zal opslaan tijdens het doorlopen van de regellus. Volgende parameters zullen op elk discreet tijdstip worden gelogd:

  • de buitentemperatuur
  • de wateraanvoertemperatuur
  • het regelcommando
  • de klepstand van de regelklep
  • het volumedebiet dat de regelklep doorlaat
  • de ruimtetemperatuur
  • de temperatuur van de bouwschil
  • de warmteafgifte van de radiator aan de ruimte
In [26]:
data_logger = DataLogger('T_out', 'T_we', 'out', 'h', 'V_w', 'T_in', 'T_bm', 'Q_e')

Nadat de regellus voltooid is, kunnen via de datalogger de resultaten worden bekeken (zie par. 6).

5. Simulatie van de regelkring

5.1 Opstellen van de tijdas

We stellen een tijdsas op die 1 etmaal (24 h) omspant. De tijdsafstand tussen 2 opeenvolgende tijdstippen is de tijdstap dt.

In [27]:
time_axis = np.arange(0.0, 24 * 3600.0 + dt, dt)

5.2 Verloop van de buitentemperatuur langs de tijdsas

We maken een temperatuurprofiel aan van de buitentemperatuur. De buitentemperatuur zal sinusvormig variëren rond een gemiddelde waarde avg, met een amplitude van ampl en een periode van period.

In [28]:
T_out = OutsideTemperature(avg=0.0, ampl=5.0, period=24 * 3600.0, profile='sine')

5.3 Opgave van de initiële waarden van de ruimtetemperatuur en de bouwschiltemperatuur

Het berekeningsalgoritme heeft (omwille van de numerieke benadering van de eerste afgeleide) van de ruimtetemperatuur en de bouwschiltemperatuur twee voorafgaande beginwaarden nodig (d.w.z. op de tijdstippen t = -2.dt en t = -1.dt).

In [29]:
room.initial_values(T_r_ini=[T_out.avg] * 2, T_bm_ini=[T_out.avg] * 2)

5.4 Meetvertraging toevoegen aan de regelkring

Er kan wat tijd overgaan alvorens een verandering van de ruimtetemperatuur door de regelaar wordt gemeten. Een 'dode tijd' of looptijd is in het programma geïmplementeerd als een FIFO-buffer. De lengte van de buffer bepaalt het aantal tijdstappen dat het duurt voordat de op het tijdstip t gemeten ruimtetemperatuur wordt doorgegeven aan de regelaar.

In [30]:
m_delay = DeadTime(2, T_out.avg)  # 2: de lengte van de FIFO-buffer (2 tijdstappen), T_out.avg = initiële waarden in de buffer

5.5 Berekening van het dynamisch verloop van de ruimtetemperatuur in de tijd

De regelkring wordt opgestart met de initiële waarde van de ruimtetemperatuur op het tijdstip t = -1.dt die aan de regelaar wordt toegevoerd. De regelaar bepaalt het regelcommando (in procenten). Dit regelcommando stemt overeen met de gevraagde kleppositie van de regelklep en wordt toegevoerd aan de klepmotor. De klepmotor drijft de regelklep aan. De bereikte klepstand bepaalt het volumedebiet dat de regelklep doorlaat tussen de tijdstippen t en t+dt. Op basis van dit volumedebiet, de wateraanvoertemperatuur en de buitentemperatuur wordt de nieuwe ruimtetemperatuur op het tijdstip t+dt berekend (alsook de bouwschiltemperatuur en de warmteafgifte van de radiator). Deze nieuwe waarde wordt dan vooraan in de meetvertraging (FIFO-buffer) gestopt en de laatste waarde in de FIFO-buffer wordt aan de regelaar toegevoerd. De regllus wordt dan herhaald tot het einde van de tijdas is bereikt.

We zullen de regellus (for-lus) een aantal keer doorlopen (num_cycles). In de laatste cyclus (num_cycles = 1) voeren we op 6h een setpointverlaging in op de regelaar en op 12h zetten we het setpoint terug op de ontwerp-binnentemperatuur. In de laatste cyclus schrijven we de parameters van de regelkring naar de datalogger.

De variabele outdoor_reset wordt aangewend om al dan niet een variabele wateraanvoertemperatuur i.f.v. de buitentemperatuur te gebruiken. Indien True zal de wateraanvoertemperatuurregelaar (cf. par. 3.2) de wateraanvoertemperatuur bepalen. Indien False wordt de wateraanvoertemperatuur op een constante waarde gehouden.

In [31]:
outdoor_reset = True  # True: outdoor reset control is actief, False: wateraanvoertemperatuur is constant en gelijk aan ontwerpwaarde

num_cycles = 4
while num_cycles > 0:
    # initialisatie van de regelkring met de ingestelde initiële waarde of de laatste waarde uit de vorige cyclus
    T_in = room.T_r[-1]
    
    # regellus
    for t in time_axis:
        if num_cycles == 1:
            if t == 6 * 3600.0:
                on_off_controller.set_point(T_in_des - 3.0)
            if t == 12 * 3600.0:
                on_off_controller.set_point(T_in_des)
        # regelcommando tussen t en t+dt
        out = on_off_controller(t, T_in)               
        # klepstand tussen t en t+dt
        h = valve_motor(out)                           
        # volumedebiet tussen t en t+dt
        V_w = control_valve(h)                         
        # buitentemperatuur tussen t en t+dt
        T_out_ = T_out(t)                              
        if outdoor_reset is True:
            # wateraanvoertemperatuur wordt door temperatuurregelaar berekend
            T_we = outdoor_reset_controller(T_out_)    
        else:
            # wateraanvoertemperatuur blijft constant
            T_we = room.radiator.nominal_specs['Twe']
        # ruimtetemperatuur, bouwschiltemperatuur en warmteafgifte in de ruimte op tijdstip t+dt
        T_in, T_bm, Q_e = room(V_w, T_we, T_out_)      
        # ruimtetemperatuur op het tijdstip t + dt dat de regelaar meet (t.g.v. meetvertraging)
        T_in = m_delay(T_in)                           
        if num_cycles == 1:
            data_logger.log(t / 3600.0, T_out=T_out_, T_we=T_we, out=out, h=h, V_w=V_w * 6.0e4, T_in=T_in, T_bm=T_bm, Q_e=Q_e)
            
    num_cycles -= 1

6. De resultaten

De gelogde data wordt aan de datalogger opgevraagd. Daarmee worden 3 grafieken aangemaakt:

  • De eerste grafiek toont het tijdsverloop van de temperatuur van het verwarmingswater, van de ruimte, van de bouwschil en van de buitentemperatuur.
  • De tweede grafiek toont het tijdsverloop van de warmteafgifte van de radiator.
  • De derde grafiek toont het tijdsverloop van het regelcommando en de kleppositie.
In [32]:
data = data_logger.get_data()
In [33]:
graph = graphing.MultiGraph(row_num=3, col_num=1, fig_size=[10.0, 15.0], dpi=96)

graph[1].add_data_set('T_out', data['t'], data['T_out'])
graph[1].add_data_set('T_bm', data['t'], data['T_bm'])
graph[1].add_data_set('T_in', data['t'], data['T_in'])
graph[1].add_data_set('T_we', data['t'], data['T_we'])
graph[1].add_legend()
graph[1].set_axis_titles('time (h)', 'T_out, T_bm, T_in, T_we (°C)')
graph[1].scale_x_axis(data.iloc[0, 0], data.iloc[-1, 0], 2.0)
graph[1].scale_y_axis(-10.0, 80.0, 5.0)
graph[1].turn_grid_on()
graph[1].draw_graph()

graph[2].add_data_set('Qe', data['t'], data['Q_e'])
graph[2].set_axis_titles('time (h)', 'Q_e (W)')
graph[2].scale_x_axis(data.iloc[0, 0], data.iloc[-1, 0], 2.0)
graph[2].turn_grid_on()
graph[2].draw_graph()

graph[3].add_data_set('out', data['t'], data['out'])
graph[3].add_data_set('h', data['t'], data['h'])
graph[3].add_legend()
graph[3].set_axis_titles('time (h)', 'out, h (%)')
graph[3].scale_x_axis(data.iloc[0, 0], data.iloc[-1, 0], 2.0)
graph[3].turn_grid_on()
graph[3].draw_graph()

graph.show_graph()

Via onderstaande link-knop kan men een webapplicatie opstarten waarmee men met de regelkring interactief kan experimenteren. Het kan wel een paar minuten duren alvorens de webapplicatie volledig is opgestart (de applicatie draait op een publieke server mybinder.org). Op de webpagina die zal verschijnen, selecteer "on_off_control". Er zal dan een volgende webpagina openen. Klik daar op "on_off_control.ipynb". De eigenlijke webapplicatie zal nu opstarten. Het kan even duren voordat de gebruikersinterface volledig zichtbaar wordt. Het programma berekent namelijk eerst een simulatie met standaard waarden. Uiteindelijk zal een invulformulier op het scherm verschijnen. Door parameterwaarden te wijzigen, bv. de gemiddelde buitentemperatuur of de coëfficiënten van de wateraanvoertemperatuurregelkarakteristiek (outdoor reset line) kan men nagaan welk effect dit zal hebben op het gedrag van de regelkring. Men kan ook de radiator, het ruimtemodel, de regelparameters van de aan/uit-regelaar, etc. veranderen. Wanneer op de 'submit'-knop wordt gedrukt, wordt de simulatie gemaakt en de resultaten afgebeeld in grafieken zoals hierboven.

Binder