In [1]:
import dependencies
import cmath
import numpy as np
from hvac.heat_loss_calc import *
from nummath import linearsystem
In [2]:
from IPython.display import HTML
HTML('<style>{}</style><p>Loaded <code>my_styles.css</code></p>'.format(open('my_styles.css').read()))
Out[2]:

Loaded my_styles.css

EFFECTIEVE THERMISCHE CAPACITEIT VAN EEN BUITENMUUR

Zie afbeelding: we beschouwen een buitenmuur die is samengesteld van buiten (links) naar binnen (rechts) uit:

  • een gevelbaksteen (b x h x d = 188 x 65 x 88 mm) en cementvoeg (12 mm)
  • een matig verluchte luchtspouw (20 mm)
  • een isolatielaag (60 mm)
  • een snelbouwbaksteen (b x h x d = 288 x 138 x 138 mm) en cementvoeg (12 mm)
  • een pleisterlaag (10 mm)

Het dynamisch warmtetransport doorheen een muur kan men berekenen door de muur op te vatten als een lineair thermisch netwerk. Daartoe wordt de muur in denkbeeldige lagen onderverdeeld die geassocieerd kunnen worden aan temperatuurknopen in een netwerk. Deze temperatuurknopen zijn dan met elkaar verbonden door de thermische weerstanden van de lagen. Hoe groter het aantal lagen waarin de muur wordt onderverdeeld, hoe nauwkeuriger men het dynamisch warmtetransport door de muur kan simuleren. Een lineair thermisch netwerk dat is samengesteld uit n temperatuurknopen wordt een nN-model (n-de orde systeem) van de muur genoemd. De bedoeling bestaat erin om het nN-model van de muur te reduceren tot een eenvoudig, evenwaardig 1N-model (1ste orde systeem). Daartoe dient de thermische capaciteit van de temperatuurknoop in het 1N-model bepaald. Deze thermische capaciteit wordt de effectieve thermische capaciteit van de muur genoemd. Deze kan aanzienlijk kleiner uitvallen dan de statische thermische capaciteit van de muur.

1. Berekening van de thermische weerstand en de statische thermische capaciteit van de buitenmuur

1.1 Verklaring symbolen

symbool verklaring eenheid
A oppervlakte m²
t dikte m
k warmtegeleidingscoëfficiënt W/(m².K)
rho massadichtheid kg/m³
cm specifieke warmtecapaciteit per kg J/(kg.K)
r specifieke thermische weerstand (m².K)/W
ca specifieke thermische capaciteit per m² J/(m².K)

NOOT
De specifieke thermische capaciteit per m² ca volgt uit het produkt:

ca = rho * cm * t [kg/m³ * J/(kg.K) * m = J/(m².K)]

1.2 Configuratie van de muur

Buitenblad
Het buitenblad is samengesteld uit gevelbakstenen met daartussen cementvoegen. Voorgesteld in een thermisch netwerk is dit een parallelschakeling van 2 thermische weerstanden.

In [3]:
brick_ext = BuildingElement(
    A=188.0e-3 * 65.0e-3,  # oppervlakte van 1 baksteen
    t=88.0e-3,             # dikte van 1 baksteen
    k=0.91, 
    rho=1500.0, 
    cm=840.0
)

joint_ext = BuildingElement(
    A=12.0e-3 * (188.0e-3 + 12.0e-3) + 12.0e-3 * 65.0e-3,  # oppervlakte van de cementvoeg rond 1 baksteen (1 langse voeg + 1 kopse voeg)
    t=88.0e-3, 
    k=1.5, 
    rho=1800.0, 
    cm=840.0
)

leaf_ext = BuildingCompositeElement(brick_ext, joint_ext)

Luchtspouw

In [4]:
air_cavity = BuildingElement(
    t=20.0e-3, 
    r=0.085, 
    rho=1.205, 
    cm=1005.0
)

Isolatielaag

In [5]:
insulation = BuildingElement(
    t=60.0e-3, 
    k=0.041, 
    rho=25.0, 
    cm=840.0, 
    corr_r=-0.1  # correctiefactor voor de plaatsing van de isolatie
)

Binnenblad

In [6]:
brick_int = BuildingElement(
    A=288.0e-3 * 138.0e-3, 
    t=138.0e-3, 
    k=0.32, 
    rho=1100.0, 
    cm=840.0
)

joint_int = BuildingElement(
    A=12.0e-3 * (288.0e-3 + 12.0e-3) + 12.0e-3 * 138.0e-3, 
    t=138.0e-3, 
    k=1.0, 
    rho=1900.0, 
    cm=840.0
)

leaf_int = BuildingCompositeElement(brick_int, joint_int)

Pleisterlaag

In [7]:
stucco = BuildingElement(
    t=10.0e-3, 
    k=0.57, 
    rho=1300.0, 
    cm=840.0
)

Complete buitenmuur
Nadat de samenstellende delen van de buitenmuur zijn gespecifieerd in het programma, kan de complete buitenmuur in het programma gecreëerd worden.

In [8]:
wall = BuildingPart(leaf_ext, air_cavity, insulation, leaf_int, stucco)

1.3 Thermische weerstand en statische thermische capaciteit van de muur (per vierkante meter)

In [9]:
display(HTML(
    '<ul>'
    f"<li>Specifieke thermische weerstand van de muur = <b>{wall.r:.3f}</b> (m^2.K)/W</li>"
    f"<li>Specifieke statische thermische capaciteit van de muur = <b>{wall.ca:.3e}</b> J/(m^2.K)</li>"
    '</ul>'
))
  • Specifieke thermische weerstand van de muur = 1.897 (m^2.K)/W
  • Specifieke statische thermische capaciteit van de muur = 2.660e+05 J/(m^2.K)

2. Opstellen nN-model van de buitenmuur

De muur zal nu in smalle verticale lagen onderverdeeld worden. Elke laag kan met een temperatuurknoop Tiworden geassocieerd in het lineair thermisch netwerk, waaraan de statische thermische capaciteit van de laag is gekoppeld. De temperatuurknopen zijn onderling verbonden door de thermische weerstand van de lagen tussen elke twee opeenvolgende knopen. Onderstaande figuur geeft het lineair thermisch netwerk weer van een muur samengesteld uit n temperatuurknopen (zgn. nN-model van de muur). To is de temperatuurbron die een sinusoïdaal wisselende buitentemperatuur genereert. qi zijn de warmtestromen (warmtefluxen) die in het netwerk vloeien tussen de temperatuurknopen.

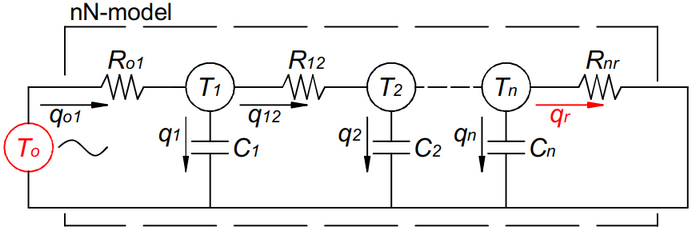
Concreet wordt het buitenblad in 4 lagen onderverdeeld, de luchtspouw blijft 1 laag, de isolatielaag wordt onderverdeeld in 3 lagen, het binnenblad in 6 lagen en de pleisterlaag blijft ook 1 laag.

In [10]:
# aantal lagen = aantal temperatuurknopen van het lineair thermisch netwerk
n_wall_ext = 4    # gevelblad
n_air_cavity = 1  # luchtspouw
n_insulation = 3  # isolatielaag
n_wall_int = 6    # binnenblad
n_stucco = 1      # pleisterlaag
n = [n_wall_ext, n_air_cavity, n_insulation, n_wall_int, n_stucco]

2.1 Berekening van de thermische weerstand en de statische thermische capaciteit van elke laag

Convectieweerstand aan de buitenzijde van de muur

In [11]:
r_conv_o = 0.04

Buitenbladlagen

In [12]:
r_layer_we = leaf_ext.r / n_wall_ext
ca_layer_we = leaf_ext.ca / n_wall_ext

Luchtspouwlagen

In [13]:
r_layer_ac = air_cavity.r / n_air_cavity
ca_layer_ac = air_cavity.ca / n_air_cavity

Isolatielagen

In [14]:
r_layer_ins = insulation.r / n_insulation
ca_layer_ins = insulation.ca / n_insulation

Binnenbladlagen

In [15]:
r_layer_wi = leaf_int.r / n_wall_int
ca_layer_wi = leaf_int.ca / n_wall_int

Pleisterlagen

In [16]:
r_layer_st = stucco.r / n_stucco
ca_layer_st = stucco.ca / n_stucco

Convectieweerstand aan de binnenzijde van de muur

In [17]:
r_conv_i = 0.13

2.2 Configuratie van de lagen/temperatuurknopen

In [18]:
layers = []
for i in range(0, sum(n)):
    if 0 <= i < n[0]:
        layers.append(BuildingElement(r=r_layer_we, ca=ca_layer_we))
    if n[0] <= i < sum(n[:2]):
        layers.append(BuildingElement(r=r_layer_ac, ca=ca_layer_ac))
    if sum(n[:2]) <= i < sum(n[:3]):
        layers.append(BuildingElement(r=r_layer_ins, ca=ca_layer_ins))
    if sum(n[:3]) <= i < sum(n[:4]):
        layers.append(BuildingElement(r=r_layer_wi, ca=ca_layer_wi))
    if sum(n[:4]) <= i < sum(n):
        layers.append(BuildingElement(r=r_layer_st, ca=ca_layer_st))

2.3 Berekening van de thermische weerstanden tussen opeenvolgende temperatuurknopen

De temperatuurknopen situeren zich in het midden van een laag. De thermische weerstand tussen twee opeenvolgende knopen bestaat daarom uit de helft van de thermische weerstand van de ene laag en uit de helft van de thermische weerstand van de volgende laag. Tussen de temperatuurbron To van het lineair thermisch netwerk en het eerste knooppunt bevindt zich nog de convectieweerstand r_conv_o.

In [19]:
r = [r_conv_o + 0.5 * layers[0].r]
for i in range(1, sum(n)):
    r.append(0.5 * (layers[i-1].r + layers[i].r))
r.append(0.5 * layers[-1].r + r_conv_i)

2.4 Berekening van de thermische capacitantie van de temperatuurknopen

We beschouwen een sinusoïdaal variërende buitentemperatuur To aan de buitenzijde van de muur en een constante binnentemperatuur Tr aan de binnenzijde van de muur, waarbij de gemiddelde waarde van de sinusvormig variërende buitentemperatuur gelijk is aan de constante waarde van de binnentemperatuur. In die specifieke situatie is het lineair thermisch netwerk vanuit wiskundig oogpunt analoog aan een elektrisch wisselstroomnetwerk dat is samengesteld uit weerstanden en condensatoren. De netwerkoplossingsmethoden uit de wisselstroomtheorie kunnen hier nu evengoed aangewend worden om de warmtestromen tussen de temperatuurknopen te bepalen.

De complexe capacitantie van de temperatuurknopen
Uit de wisselstroomtheorie volgt dat de complexe impedantie of capacitantie van een condensator C bepaald wordt door de formule:

$$ {X_C} = \frac{1}{{j\omega C}} $$

Daarin is $ {\omega} $ de cirkelfrequentie van de wisselspanning en wisselstroom. We stellen de periode van de sinusoïdale buitentemperatuur To vast op 1 etmaal of 24 h.

In [20]:
# cirkelfrequentie [rad/s] van de sinusvormig variërende buitentemperatuur (periode = 24 h)
w = 2.0 * np.pi / (24 * 3600.0)

# thermische complexe capacitantie van de temperatuurknopen
xc = [1.0 / (w * layers[i].ca * 1.0j) for i in range(sum(n))]

2.5 Opstellen van de coëfficiëntenmatrix A en de inputvector B van het lineair thermisch netwerk

De bedoeling is voor een gegeven sinusvormig verloop van de buitentemperatuur To aan de buitenzijde van de muur te bepalen welke de warmteflux qrzal zijn aan de binnenzijde van de muur. Om de warmtestromen te vinden tussen de temperatuurknopen van het thermisch netwerk dient een stelsel van 2n+1 vergelijkingen in 2n+1 onbekende warmtestromen opgelost te worden. Deze vergelijkingen volgen uit de luswet en knooppuntwet van Kirchoff uit de electriciteitstheorie.

Complexe voorstelling van de sinusoïdale buitentemperatuur To_ampl * sin(w*t)

In [21]:
To_ampl = 5.0
To = cmath.rect(To_ampl, -np.pi / 2.0)

Opstellen van de coëfficiëntenmatrix van het stelsel vergelijkingen

In [22]:
n = sum(n)
A = np.zeros((2 * n + 1, 2 * n + 1), dtype=complex)
for i, j in zip(range(0, n + 1), range(0, 2 * n + 1, 2)):
    A[i, j] = -r[i]
    if j < 2 * n:
        A[i, j+1] = -xc[i]
    if i > 0 and j > 0:
        A[i, j-1] = xc[i-1]
for i, j in zip(range(n + 1, 2 * n + 1), range(1, 2 * n, 2)):
    A[i, j] = -1.0
    A[i, j-1] = 1.0
    A[i, j+1] = -1.0

Opstellen van de inputvector van het stelsel vergelijkingen

In [23]:
B = np.zeros((2 * n + 1, 1), dtype=complex)
B[0] = -To

2.6 Oplossen van het stelsel lineaire vergelijkingen

In [24]:
X = linearsystem.GaussElimin(A, B, pivot_on=True, dtype=complex).solve()

3. Afleiding van een evenwaardig 1N-model van de muur

We zijn in feite alleen maar geïnteresseerd in de warmteflux aan de binnenzijde van de muur. We wensen namelijk een 1N-model van de muur te bekomen dat 'evenwaardig' is met het nN-model van de muur. Het 1N-model is evenwaardig als voor een zelfde amplitude van de sinusoïdale buitentemperatuur dezelfde warmteflux wordt veroorzaakt aan de binnenzijde van de muur als in het nN-model. Het is deze warmteflux, die in of uit de muur stroomt, die de thermische belasting t.a.v. de klimaatinstallatie zal uitmaken. Het komt er dan vervolgens op aan de thermische capaciteit te vinden in het 1N-model, zodat de bovenstaande voorwaarde wordt vervuld.

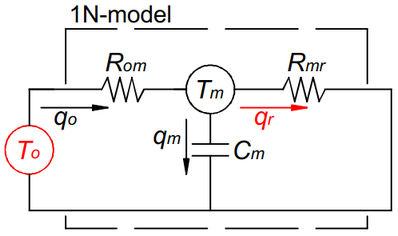
3.1 De dynamische warmteflux aan de binnenzijde van de muur

De dynamische warmteflux qraan de binnenzijde van de muur is het laatste element in de oplossingenvector X.

In [25]:
qr = X[-1]
qr_ampl = abs(qr)
qr_phi = cmath.phase(qr)
display(HTML(f"De amplitude van de warmteflux aan de binnenzijde van de muur = <b>{qr_ampl:.3f}</b> W/m²."))
De amplitude van de warmteflux aan de binnenzijde van de muur = 0.802 W/m².

Noot
Vergelijk deze uitkomst met de amplitude van de warmteflux die volgt uit een stationaire beschouwing. De thermische capaciteit of thermische massa van de muur dempt in werkelijkheid de amplitude van de warmteflux. In een stationaire beschouwing wordt daarmee geen rekening gehouden.

In [26]:
# stationaire warmteflux aan de binnenzijde van de muur
qr_ampl_stat = To_ampl / (r_conv_o + wall.r + r_conv_i)
display(HTML(f" De amplitude van de stationaire warmteflux aan de binnenzijde van de muur = <b>{qr_ampl_stat:.3f}</b> W/m²."))
De amplitude van de stationaire warmteflux aan de binnenzijde van de muur = 2.419 W/m².

3.2 Berekening van de thermische weerstanden in het 1N-model

De thermische weerstand tussen de temperatuurknoop Tm en de binnenlucht

In [27]:
r_mr = 0.5 * wall.r + r_conv_i

De thermische weerstand tussen de buitenlucht en de temperatuurknoop Tm

In [28]:
r_om = 0.5 * wall.r + r_conv_o

3.3 Berekening van de thermische capaciteit van de temperatuurknoop Tm

Warmteflux aan de buitenzijde van de muur

In [29]:
qo_ampl = (abs(To) - r_mr * qr_ampl) / r_om
qo_phi = np.arctan2(
    np.sin(np.pi / 2.0 + qr_phi) + qr_ampl * np.sin(qr_phi),
    np.cos(np.pi / 2.0 + qr_phi) + qr_ampl * np.cos(qr_phi)
)

Warmteflux die in de thermische capaciteit van de muur wordt opgeslagen

In [30]:
qm_ampl = np.sqrt(
    (qo_ampl * np.cos(qo_phi) - qr_ampl * np.cos(qr_phi)) ** 2
    + (qo_ampl * np.sin(qo_phi) - qr_ampl * np.sin(qr_phi)) ** 2
)

Effectieve thermische capaciteit van de muur

In [31]:
ca_eff = qm_ampl / (w * r_mr * qr_ampl)
display(HTML(f"De effectieve thermische capaciteit van de muur bedraagt= <b>{ca_eff:.3e}</b> J/(m².K)."))
De effectieve thermische capaciteit van de muur bedraagt= 5.936e+04 J/(m².K).

NOOT
Noteer dat de berekende 'effectieve' thermische capaciteit van de muur in enige mate zal afhangen van zowel de amplitude als de frequentie (periode) van de sinusvormig variërende buitentemperatuur. Het lijkt vanzelfsprekend dat een periode van 24 h (1 etmaal) voor de sinusoïdale buitentemperatuur het meest voor de hand ligt.

In [ ]: