Design of a Hydronic Pipe Network
Contents
Design of a Hydronic Pipe Network#
This notebook demonstrates how a hydronic distribution system for heating can be designed with the hvac.fluid_flow package.
Let’s Import What We’ll Need#
from hvac import Quantity
from hvac.fluid_flow import PipeNetwork, PipeScheduleFactory
from hvac.fluids import Fluid
Q_ = Quantity
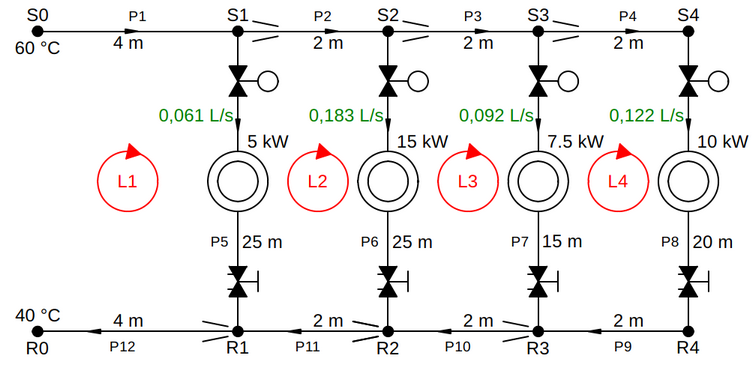
Hydronic Network Scheme#
Define the Fluid in the Pipe Network#
In a hydronic heating system water is being used as the heat carrier to transport heat from the heat generator(s) to the heat emitters.
Water = Fluid('Water')
heating_water = Water(T=Q_(50, 'degC'), P=Q_(2, 'bar'))
Configuration of the Pipe Network#
The configuration of a fluid flow network can be done in a spreadsheet program, like Excel or OpenOffice Calc. Each row of the spreadsheet table represents a pipe in the network. The interconnection of pipes in the network happens with nodes. Each pipe has a start node and an end node, as shown by the dots in the network scheme above. The nodes allow the program to find out how the pipes in the network are interconnected. The first row of the spreadsheet table is the header. The header labels cannot be chosen freely; they must be known by the program. In the code block below the spreedsheet table for this example is displayed to show you how the table looks like in the spreadsheet program:
import pandas as pd
table = pd.read_csv('./networks/ex1_closed-pipe-network-design.csv')
ja.display_table(table)
| conduit_ID | start_node_ID | end_node_ID | loop_ID | schedule | length | volume_flow_rate | specific_pressure_drop | |
|---|---|---|---|---|---|---|---|---|
| 0 | P1 | S0 | S1 | L1 | copper | 4 | 0.458 | 0.2 |
| 1 | P2 | S1 | S2 | L2 | copper | 2 | 0.397 | 0.2 |
| 2 | P3 | S2 | S3 | L3 | copper | 2 | 0.214 | 0.2 |
| 3 | P4 | S3 | S4 | L4 | copper | 2 | 0.122 | 0.2 |
| 4 | P5 | S1 | R1 | (L1, L2) | pex | 25 | 0.061 | 0.2 |
| 5 | P6 | S2 | R2 | (L2, L3) | pex | 25 | 0.183 | 0.2 |
| 6 | P7 | S3 | R3 | (L3, L4) | pex | 15 | 0.092 | 0.2 |
| 7 | P8 | S4 | R4 | L4 | pex | 20 | 0.122 | 0.2 |
| 8 | P9 | R4 | R3 | L4 | copper | 2 | 0.122 | 0.2 |
| 9 | P10 | R3 | R2 | L3 | copper | 2 | 0.214 | 0.2 |
| 10 | P11 | R2 | R1 | L2 | copper | 2 | 0.397 | 0.2 |
| 11 | P12 | R1 | R0 | L1 | copper | 4 | 0.458 | 0.2 |
This table is used to design a pipe network. When designing a pipe network the length and the design volume flow rate of each pipe are already known. A reasonble specific pressure drop needs to be chosen for each pipe. In this case a specific pressure drop of 0.2 kPa/m has been selected. Notice that there are no measuring units mentioned in the table. We can use any appropriate unit we want for a certain quantity, but later on we will have to tell the program what these units are. In the last column schedule a name has been entered that refers to a collection of commercially available pipe sizes. More explanation about this feature will follow, but first a worth about the header labels:
The column conduit_ID contains a reference name or ID for each pipe in the network.
The column start_node_ID specifies the ID of the pipe’s start node, i.e. the node where the fluid leaves.
The column end_node_ID specifies the ID of the pipe’s end node, i.e. the node where the fluid arrives.
The column loop_ID is not required, and thus optional, when designing a pipe network, but we will need this if we want to analyze our network later on with the Hardy Cross method. This will be explained in a subsequent notebook where we will analyze the behaviour of the network when control valves get more closed.
The column schedule contains a reference name (that you can choose freely) to a collection of commercially available pipe sizes. When designing a network this column is optional. You can also assign only one schedule to the whole network, if all pipes in the network are of the same type. Or you could omit the schedule, but then you’ll get calculated, theoretical pipe diameters returned, which probably won’t be commercially available.
The column length contains the length of each pipe (expressed in the unit you prefer)
The column volume_flow_rate contains the design volume flow rate in each pipe (expressed in the unit you prefer)
The column specific_pressure_drop contains the pressure drop per unit pipe length (expressed in the units you prefer)
These header labels are needed when designing a pipe network. But there are more header labels defined in the program that can or will be needed when designing a duct network or when analyzing an existing pipe or duct network. These additional header labels will be discussed in subsequent notebooks.
IMPORTANT!
When the table in the spreadsheet program is ready, you must save it as a comma-separated-values (csv) file, as this is the only file format that can be loaded by the program. Also be aware for the decimal point. It must be a point, not a comma! If the latter case is true, you can easily change this in the spreadsheet program, e.g. by selecting the table or the whole sheet and then changing the language formatting of the spreadsheet cells to any language format that uses a point to separate the decimals of a number before saving as a csv-file.
Sizing the Pipes in the Network#
Loading the Pipe Schedules#
As can be seen in the table above, we use two different reference names to reference two different collections of commercially available pipes, that are called “schedules”. As one could have guessed, “copper” refers to copper tubes, while “pex” refers to PEX-AL-PEX tubing.
Any schedule you want can be used by the program. For this you need to make a “schedule table” in a spreadsheet program. The following code shows a fragment of the spreadsheet table for “copper”:
schedule_table = pd.read_excel(
io="./pipe-schedule-data/copper_tube.ods",
sheet_name=0,
header=0
)
ja.display_table(schedule_table.head())
| D_nom | D_ext | t | D_int | |
|---|---|---|---|---|
| 0 | 10.0 | 10.0 | 1.0 | 8.0 |
| 1 | 12.0 | 12.0 | 1.0 | 10.0 |
| 2 | 15.0 | 15.0 | 1.0 | 13.0 |
| 3 | 18.0 | 18.0 | 1.0 | 16.0 |
| 4 | 22.0 | 22.0 | 1.0 | 20.0 |
As you can see, the header of the spreadsheet table must have these 4 labels:
the column labeled D_nom contains the available nominal pipe diameters
the column labeled D_ext contains the corresponding exterior diameters
the column labeled t contains the corresponding pipe wall thicknesses
the column labeled D_int contains the corresponding interior diameters
The values can be expressed in any appropriate measuring unit you prefer, however this unit must be the same for all values in the table.
Having the spreadsheet files saved at a known file location, we can now create the schedules as follows:
copper_schedule = PipeScheduleFactory.get(
name='copper',
file_path='./pipe-schedule-data/copper_tube.ods',
unit='mm'
)
We assign the reference name we have used in the pipe network configuration file to the parameter name. Next we specify the file path where the schedule file is stored and the unit in which we have expressed the values of the pipe diameters in the table. (The default unit is ‘mm’, so we could have omitted the parameter unit here, however we included it for completeness.) Now we can do exactly the same thing to create our “pex” schedule:
pex_schedule = PipeScheduleFactory.get(
name='pex',
file_path='./pipe-schedule-data/henco_standard_pex.ods',
)
Creating the Closed Pipe Network#
pipe_network = PipeNetwork.create(
ID='heating_system',
fluid=heating_water,
wall_roughness=Q_(0.0015, 'mm'),
schedule=None,
start_node_ID='S0',
end_node_ID='R0'
)
A pipe network is created by calling the class method create of the PipeNetwork class. The code block above shows which parameters the method needs to create a closed pipe network. A closed pipe network is a network that has a start node, where all fluid enters the network, and that has only one end node, where all fluid leaves the network. (It is also possible to configure an open pipe network, which has multiple end nodes, e.g. a drinking water distrubution system, which will be demonstrated in a subsequent notebook).
Through parameter wall_roughness the absolute pipe wall roughness of all pipes in the network is set. If not all pipes in the network have the same absolute roughness, you can add a column wall_roughness to the pipe network configuration file and then set the parameter wall_roughness in the call to method create to None.
The parameter schedule has been set to None, as not all pipes in the network belong to the same schedule.
Setting Units#
Before moving on, we must make sure that the program will do the calculations with the units we had in mind when we wrote the pipe network configuration file. Units can be set through the attribute units of the PipeNetwork instance we’ve just created. Units can be assigned to the following quantities:
quantity |
keyword |
default unit |
|---|---|---|
pipe length |
‘length’ |
‘m’ |
diameter |
‘diameter’ |
‘mm’ |
width (duct) |
‘dim_width’ |
‘mm’ |
height (duct) |
‘dim_height’ |
‘mm’ |
volume flow rate |
‘volume_flow_rate’ |
‘m ** 3 / s’ |
flow velocity |
‘velocity’ |
‘m / s’ |
pressure (difference) |
‘pressure’ |
‘Pa’ |
specific pressure drop |
‘specific_pressure’ |
‘Pa / m’ |
pressure head |
‘pressure_head |
‘Pa’ |
altitude (elevation) |
‘height’ |
‘m’ |
absolute pipe wall roughness |
‘wall_roughness’ |
‘mm’ |
pump or fan coefficients |
‘machine_coefficients’ |
[‘Pa’, ‘Pa / (m ** 3 / s)’, ‘Pa / (m ** 3 / s) ** 2’] |
In our example volume flow rate is expressed in units of L/s, and specific pressure drop in units of kPa/m. Furthermore, we want pressures and pressure differences be expressed in units of kPa.
pipe_network.units['volume_flow_rate'] = 'L / s'
pipe_network.units['pressure'] = 'kPa'
pipe_network.units['specific_pressure'] = 'kPa / m'
Load the Pipe Network Configuration File into the PipeNetwork Instance#
pipe_network.load_from_csv('./networks/ex1_closed-pipe-network-design.csv')
When the method load_from_csv is called, the program will immediately calculate the required diameter of each pipe. We can get an overview of the pipes in the network by calling the method get_pipe_table, which returns a Pandas DataFrame object.
ja.display_table(pipe_network.get_pipe_table())
| pipe ID | L [m] | DN [mm] | Di [mm] | V [l/s] | v [m/s] | zeta | Re | Δp-dyn. [kPa] | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | P1 | 4.0 | 35.0 | 32.0 | 0.458 | 0.569476 | 0 | 32945.645835 | 0.462787 |
| 1 | P2 | 2.0 | 28.0 | 25.0 | 0.397 | 0.808762 | 0 | 36553.841457 | 0.584486 |
| 2 | P3 | 2.0 | 22.0 | 20.0 | 0.214 | 0.681183 | 0 | 24630.107279 | 0.568306 |
| 3 | P4 | 2.0 | 18.0 | 16.0 | 0.122 | 0.606778 | 0 | 17551.828785 | 0.612130 |
| 4 | P5 | 25.0 | 18.0 | 14.0 | 0.061 | 0.396263 | 0 | 10029.616449 | 4.297709 |
| 5 | P6 | 25.0 | 26.0 | 20.0 | 0.183 | 0.582507 | 0 | 21062.194542 | 5.390640 |
| 6 | P7 | 15.0 | 20.0 | 16.0 | 0.092 | 0.457570 | 0 | 13235.805313 | 2.799807 |
| 7 | P8 | 20.0 | 20.0 | 16.0 | 0.122 | 0.606778 | 0 | 17551.828785 | 6.121301 |
| 8 | P9 | 2.0 | 18.0 | 16.0 | 0.122 | 0.606778 | 0 | 17551.828785 | 0.612130 |
| 9 | P10 | 2.0 | 22.0 | 20.0 | 0.214 | 0.681183 | 0 | 24630.107279 | 0.568306 |
| 10 | P11 | 2.0 | 28.0 | 25.0 | 0.397 | 0.808762 | 0 | 36553.841457 | 0.584486 |
| 11 | P12 | 4.0 | 35.0 | 32.0 | 0.458 | 0.569476 | 0 | 32945.645835 | 0.462787 |
Add Fittings to the Pipe Network#
After all the pipe diameters in the network are calculated, we can add fittings to these pipes. To add fittings to a pipe we need to import the module hvac.fluid_flow.fittings.pipe:
from hvac.fluid_flow.fittings import pipe as pipe_fittings
Tees#
For a number of pipe fittings and valves the resistance coefficient can be calculated according to the formulas in the well-known technical guide TP-410M published by Crane. These fittings and valves are located in the module crane.py of the above mentioned package. In the following we will add tees at the nodes of the cross-overs in the network. On the supply side of the network (with the ‘Sx’ labeled nodes in the scheme above) the fluid flow at the nodes is diverging, while on the return side of the network (with the ‘Rx’ labeled nodes) the fluid flow is converging. The ‘combined pipe’ of a tee is the pipe in which the fluid flow is greatest (i.e. the sum of the flow that will go through the branch and the flow that will continue in the straight leg). To create a tee for node S1, the following code will do:
tee_S1 = pipe_fittings.Tee(
flow_pattern='diverging',
combined_pipe=pipe_network.conduits['P1'],
branch_pipe=pipe_network.conduits['P5'],
ID='TEE-S1'
)
We can access the pipes in the network through the attribute conduits, which is a dictionary of which the keys are the ID’s we gave to our pipes in the configuration file. After a tee has been created, we still need to assign the resistance coefficient of the tee to the pipes. In the case of a tee fitting we have two resistance coefficients: one in the combined leg (zeta_c) and one in the branch leg (zeta_b).
pipe_network.conduits['P1'].add_fitting(tee_S1.zeta_c, tee_S1.ID)
pipe_network.conduits['P5'].add_fitting(tee_S1.zeta_b, tee_S1.ID)
In the same way we also add diverging tees to nodes S2 and S3 and converging tees to nodes R1, R2, and R3.
tee_S2 = pipe_fittings.Tee(
flow_pattern='diverging',
combined_pipe=pipe_network.conduits['P2'],
branch_pipe=pipe_network.conduits['P6'],
ID='TEE-S2'
)
pipe_network.conduits['P2'].add_fitting(tee_S2.zeta_c, tee_S2.ID)
pipe_network.conduits['P6'].add_fitting(tee_S2.zeta_b, tee_S2.ID)
tee_S3 = pipe_fittings.Tee(
flow_pattern='diverging',
combined_pipe=pipe_network.conduits['P3'],
branch_pipe=pipe_network.conduits['P7'],
ID='TEE-S3'
)
pipe_network.conduits['P3'].add_fitting(tee_S3.zeta_c, tee_S3.ID)
pipe_network.conduits['P7'].add_fitting(tee_S3.zeta_b, tee_S3.ID)
tee_R1 = pipe_fittings.Tee(
flow_pattern='converging',
combined_pipe=pipe_network.conduits['P12'],
branch_pipe=pipe_network.conduits['P5'],
ID='TEE-R1'
)
pipe_network.conduits['P12'].add_fitting(tee_R1.zeta_c, tee_R1.ID)
pipe_network.conduits['P5'].add_fitting(tee_R1.zeta_b, tee_R1.ID)
tee_R2 = pipe_fittings.Tee(
flow_pattern='converging',
combined_pipe=pipe_network.conduits['P11'],
branch_pipe=pipe_network.conduits['P6'],
ID='TEE-R2'
)
pipe_network.conduits['P11'].add_fitting(tee_R2.zeta_c, tee_R2.ID)
pipe_network.conduits['P6'].add_fitting(tee_R2.zeta_b, tee_R2.ID)
tee_R3 = pipe_fittings.Tee(
flow_pattern='converging',
combined_pipe=pipe_network.conduits['P10'],
branch_pipe=pipe_network.conduits['P7'],
ID='TEE-R3'
)
pipe_network.conduits['P10'].add_fitting(tee_R3.zeta_c, tee_R3.ID)
pipe_network.conduits['P7'].add_fitting(tee_R3.zeta_b, tee_R3.ID)
Reducers and Enlargers#
On the supply side the diameter of pipe P1 is larger than the diameter of pipe P2, the diameter of pipe P2 is larger than the diameter of pipe P3, and the diameter of pipe P3 is larger than the diameter of pipe P4. On the return side the reverse is true. Therefore, we will add reducers on the supply side and enlargers on the return side. Reducers will be placed at the beginning of the smallest pipe (notice the use of zeta_small, i.e. the resistance coefficient of the reducer referenced to the pipe with the smaller diameter), while enlargers will be placed at the beginning of the largest pipe (notice the use of zeta_large). Parameter L is the length of the reducer or enlarger.
reducer_S1 = pipe_fittings.Reducer(
large_pipe=pipe_network.conduits['P1'],
small_pipe=pipe_network.conduits['P2'],
L=Q_(5.0, 'cm'),
ID='RED-S1'
)
pipe_network.conduits['P2'].add_fitting(reducer_S1.zeta_small, reducer_S1.ID)
reducer_S2 = pipe_fittings.Reducer(
large_pipe=pipe_network.conduits['P2'],
small_pipe=pipe_network.conduits['P3'],
L=Q_(5.0, 'cm'),
ID='RED-S2'
)
pipe_network.conduits['P3'].add_fitting(reducer_S2.zeta_small, reducer_S2.ID)
reducer_S3 = pipe_fittings.Reducer(
large_pipe=pipe_network.conduits['P3'],
small_pipe=pipe_network.conduits['P4'],
L=Q_(5.0, 'cm'),
ID='RED-S3'
)
pipe_network.conduits['P4'].add_fitting(reducer_S3.zeta_small, reducer_S3.ID)
enlarger_R1 = pipe_fittings.Enlarger(
large_pipe=pipe_network.conduits['P12'],
small_pipe=pipe_network.conduits['P11'],
L=Q_(5.0, 'cm'),
ID='ENL-R1'
)
pipe_network.conduits['P12'].add_fitting(enlarger_R1.zeta_large, enlarger_R1.ID)
enlarger_R2 = pipe_fittings.Enlarger(
large_pipe=pipe_network.conduits['P11'],
small_pipe=pipe_network.conduits['P10'],
L=Q_(5.0, 'cm'),
ID='ENL-R2'
)
pipe_network.conduits['P11'].add_fitting(enlarger_R2.zeta_large, enlarger_R2.ID)
enlarger_R3 = pipe_fittings.Enlarger(
large_pipe=pipe_network.conduits['P10'],
small_pipe=pipe_network.conduits['P9'],
L=Q_(5.0, 'cm'),
ID='ENL-R3'
)
pipe_network.conduits['P10'].add_fitting(enlarger_R3.zeta_large, enlarger_R3.ID)
Elbows#
In the nodes S4 and R4 we will add elbows. Elbows don’t have a dedicated class. You need to use the general PipeFitting class. A pipe fitting can be characterized in a number of ways:
using a flow coefficient Kv, which is usually applicable to valves
using the 3K-method, which implies that a fitting is characterized by three different resistance coefficients: zeta, zeta_d and zeta_inf
using Crane’s equivalent length ratio (ELR); see Crane TP-410M
using a single resistance coefficient zeta specified in a fittings catalog
Any of these possibilities can be used to create a PipeFitting instance (you can take a look at the source code in the module hvac.fluid_flow.fittings.pipe.general). For this example we use the ELR from Crane TP-410M.
elbow_S4 = pipe_fittings.PipeFitting(
pipe=pipe_network.conduits['P4'],
ID='ELBOW-S4',
ELR=30
)
pipe_network.conduits['P4'].add_fitting(elbow_S4.zeta, elbow_S4.ID)
elbow_R4 = pipe_fittings.PipeFitting(
pipe=pipe_network.conduits['P9'],
ID='ELBOW-R4',
ELR=30
)
pipe_network.conduits['P9'].add_fitting(elbow_R4.zeta, elbow_R4.ID)
Pipes, Fittings and Flow Paths Overview#
Pipes#
ja.display_table(pipe_network.get_pipe_table())
| pipe ID | L [m] | DN [mm] | Di [mm] | V [l/s] | v [m/s] | zeta | Re | Δp-dyn. [kPa] | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | P1 | 4.0 | 35.0 | 32.0 | 0.458 | 0.569476 | 0.007096 | 32945.645835 | 0.463923 |
| 1 | P2 | 2.0 | 28.0 | 25.0 | 0.397 | 0.808762 | -0.011416 | 36553.841457 | 0.580797 |
| 2 | P3 | 2.0 | 22.0 | 20.0 | 0.214 | 0.681183 | -0.037437 | 24630.107279 | 0.559724 |
| 3 | P4 | 2.0 | 18.0 | 16.0 | 0.122 | 0.606778 | 0.096462 | 17551.828785 | 0.629676 |
| 4 | P5 | 25.0 | 18.0 | 14.0 | 0.061 | 0.396263 | 15.814630 | 10029.616449 | 5.524549 |
| 5 | P6 | 25.0 | 26.0 | 20.0 | 0.183 | 0.582507 | 5.255931 | 21062.194542 | 6.271716 |
| 6 | P7 | 15.0 | 20.0 | 16.0 | 0.092 | 0.457570 | 5.675522 | 13235.805313 | 3.386868 |
| 7 | P8 | 20.0 | 20.0 | 16.0 | 0.122 | 0.606778 | 0.000000 | 17551.828785 | 6.121301 |
| 8 | P9 | 2.0 | 18.0 | 16.0 | 0.122 | 0.606778 | 0.084951 | 17551.828785 | 0.627582 |
| 9 | P10 | 2.0 | 22.0 | 20.0 | 0.214 | 0.681183 | 0.514415 | 24630.107279 | 0.686230 |
| 10 | P11 | 2.0 | 28.0 | 25.0 | 0.397 | 0.808762 | 0.543084 | 36553.841457 | 0.759983 |
| 11 | P12 | 4.0 | 35.0 | 32.0 | 0.458 | 0.569476 | 0.262696 | 32945.645835 | 0.504875 |
Fittings#
ja.display_table(pipe_network.get_fitting_table())
| conduit ID | fitting ID | zeta | pressure drop [kPa] | |
|---|---|---|---|---|
| 0 | P1 | TEE-S1 | 0.007096 | 0.001137 |
| 1 | P2 | TEE-S2 | -0.033184 | -0.010723 |
| 2 | P2 | RED-S1 | 0.021767 | 0.007034 |
| 3 | P3 | TEE-S3 | -0.051819 | -0.011879 |
| 4 | P3 | RED-S2 | 0.014382 | 0.003297 |
| 5 | P4 | RED-S3 | 0.011511 | 0.002094 |
| 6 | P4 | ELBOW-S4 | 0.084951 | 0.015452 |
| 7 | P5 | TEE-S1 | 16.014638 | 1.242356 |
| 8 | P5 | TEE-R1 | -0.200008 | -0.015516 |
| 9 | P6 | TEE-S2 | 3.702657 | 0.620693 |
| 10 | P6 | TEE-R2 | 1.553274 | 0.260382 |
| 11 | P7 | TEE-S3 | 4.149576 | 0.429221 |
| 12 | P7 | TEE-R3 | 1.525946 | 0.157840 |
| 13 | P9 | ELBOW-R4 | 0.084951 | 0.015452 |
| 14 | P10 | TEE-R3 | 0.481536 | 0.110387 |
| 15 | P10 | ENL-R3 | 0.032880 | 0.007537 |
| 16 | P11 | TEE-R2 | 0.502002 | 0.162221 |
| 17 | P11 | ENL-R2 | 0.041081 | 0.013275 |
| 18 | P12 | TEE-R1 | 0.188702 | 0.030234 |
| 19 | P12 | ENL-R1 | 0.073994 | 0.011855 |
Flow Paths#
ja.display_table(pipe_network.get_flow_path_table())
| path | Δp-elev. [kPa] | Δp-dyn. [kPa] | Δp-tot. [kPa] | Δp-deficit [kPa] | |
|---|---|---|---|---|---|
| 0 | P1|P2|P3|P4|P8|P9|P10|P11|P12 | 0.0 | 10.934091 | 10.934091 | 0.000000 |
| 1 | P1|P5|P12 | 0.0 | 6.493348 | 6.493348 | 4.440743 |
| 2 | P1|P2|P6|P11|P12 | 0.0 | 8.581294 | 8.581294 | 2.352797 |
| 3 | P1|P2|P3|P7|P10|P11|P12 | 0.0 | 6.942400 | 6.942400 | 3.991691 |
Calling method get_flow_path_table returns a Pandas DataFrame object with all the flow paths between the start and end node of the network. The first column Δp-elev refers to the gravity, stack or chimney effect, which is due to the difference in elevation between the start and end node of the network and due to the density difference between the fluid and the ambient air. In a closed hydronic network (closed loop) this term will always be zero. The second column Δp-dyn refers to the pressure loss due to pipe friction and dynamic effects in fittings and valves. The third column Δp-tot is the sum of the first two columns. The last column Δp-deficit refers to the difference in total pressure loss between the critical flow path (i.e. the path having the greatest pressure loss) and the other flow paths between the start and end node of the network. For the critical path this value will obviously be zero. In a perfectly balanced pipe network all flow paths will have a near zero pressure loss deficit.
Add Balancing Valves to the Cross-Overs in the Network#
Calculate Preliminary Flow Coefficients#
In a balanced network the total pressure loss along each flow path will be equal to the pressure loss along the critical path of the network, when the design flow rates flow in each pipe of the pipe network. In other words, Δp-deficit of each flow path should be close to zero. If that is the case, there will be no preferential flow paths in the network and the design flow rates will actually be flowing trough each pipe of the network.
Balancing valves are placed in the cross-overs between the supply and the return side, so that flow paths have no balancing valves in common. First, a preliminary flow or valve coefficient is calculated, such that a certain presribed pressure drop will be present across the balancing valve, when it is fully open. Normally, a pressure drop of 3 kPa is selected.
cross_over_IDs = ['P5', 'P6', 'P7', 'P8']
Kvs_pre_list = [
pipe_network.add_balancing_valve(
cross_over_ID=cross_over_ID,
pressure_drop_full_open=Q_(3, 'kPa')
)
for cross_over_ID in cross_over_IDs
]
ja.display_list([
f"balancing valve in cross-over {cross_over_ID}: preliminary Kvs = {Kvs_pre}"
for cross_over_ID, Kvs_pre in zip(cross_over_IDs, Kvs_pre_list)]
)
- balancing valve in cross-over P5: preliminary Kvs = 1.2608467334744375
- balancing valve in cross-over P6: preliminary Kvs = 3.782540200423313
- balancing valve in cross-over P7: preliminary Kvs = 1.9016049095024303
- balancing valve in cross-over P8: preliminary Kvs = 2.521693466948875
Balancing Valve Selection#
Based on the pipe size and preliminary Kvs a balancing valve can now be selected. In this example the following balancing valves were selected:
cross-over P5: Kvs = 1.33
cross-over P6: Kvs = 5.35
cross-over P7: Kvs = 2.32
cross-over P8: Kvs = 2.32
Kvs_list = [1.33, 5.35, 2.32, 2.32]
for cross_over_ID, Kvs in zip(cross_over_IDs, Kvs_list):
pipe_network.set_balancing_valve_Kvs(cross_over_ID, Kvs)
Add Control Valves to the Cross-Overs#
Calculate Preliminary Flow Coefficients#
The control valves in the cross-overs serve to control the volume flow rate through the heat emitters in the hydronic distribution system at part-load conditions. They are installed upstream of the heat emitter they control. First, a preliminary flow coefficient of the control valves is calculated based on a chosen target valve authority, which should be at least 0.5 in order to attain a good controllability of the valve.
Kvs_pre_list = [
pipe_network.add_control_valve(
cross_over_ID=cross_over_ID,
target_authority=0.5
)
for cross_over_ID in cross_over_IDs
]
ja.display_list([
f"control valve in cross-over {cross_over_ID}: preliminary Kvs = {Kvs_pre}"
for cross_over_ID, Kvs_pre in zip(cross_over_IDs, Kvs_pre_list)]
)
- control valve in cross-over P5: preliminary Kvs = 0.573935179185883
- control valve in cross-over P6: preliminary Kvs = 1.721805537557649
- control valve in cross-over P7: preliminary Kvs = 0.8656071554934628
- control valve in cross-over P8: preliminary Kvs = 1.147870358371766
Control Valve Selection#
In the same way as we did with the balancing valves, the actual control valves can now be selected and their Kvs-values be entered in the program:
Kvs_list = [0.4, 1.6, 0.63, 1.0]
for cross_over_ID, Kvs in zip(cross_over_IDs, Kvs_list):
pipe_network.set_control_valve_Kvs(cross_over_ID, Kvs)
Pipes, Fittings and Flow Paths Overview (bis)#
Pipes#
ja.display_table(pipe_network.get_pipe_table())
| pipe ID | L [m] | DN [mm] | Di [mm] | V [l/s] | v [m/s] | zeta | Re | Δp-dyn. [kPa] | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | P1 | 4.0 | 35.0 | 32.0 | 0.458 | 0.569476 | 0.007096 | 32945.645835 | 0.463923 |
| 1 | P2 | 2.0 | 28.0 | 25.0 | 0.397 | 0.808762 | -0.011416 | 36553.841457 | 0.580797 |
| 2 | P3 | 2.0 | 22.0 | 20.0 | 0.214 | 0.681183 | -0.037437 | 24630.107279 | 0.559724 |
| 3 | P4 | 2.0 | 18.0 | 16.0 | 0.122 | 0.606778 | 0.096462 | 17551.828785 | 0.629676 |
| 4 | P5 | 25.0 | 18.0 | 14.0 | 0.061 | 0.396263 | 434.804239 | 10029.616449 | 38.028212 |
| 5 | P6 | 25.0 | 26.0 | 20.0 | 0.183 | 0.582507 | 114.221187 | 21062.194542 | 24.538065 |
| 6 | P7 | 15.0 | 20.0 | 16.0 | 0.092 | 0.457570 | 289.403891 | 13235.805313 | 32.734969 |
| 7 | P8 | 20.0 | 20.0 | 16.0 | 0.122 | 0.606778 | 124.363416 | 17551.828785 | 28.742410 |
| 8 | P9 | 2.0 | 18.0 | 16.0 | 0.122 | 0.606778 | 0.084951 | 17551.828785 | 0.627582 |
| 9 | P10 | 2.0 | 22.0 | 20.0 | 0.214 | 0.681183 | 0.514415 | 24630.107279 | 0.686230 |
| 10 | P11 | 2.0 | 28.0 | 25.0 | 0.397 | 0.808762 | 0.543084 | 36553.841457 | 0.759983 |
| 11 | P12 | 4.0 | 35.0 | 32.0 | 0.458 | 0.569476 | 0.262696 | 32945.645835 | 0.504875 |
Fittings and Valves#
ja.display_table(pipe_network.get_fitting_table())
| conduit ID | fitting ID | zeta | pressure drop [kPa] | |
|---|---|---|---|---|
| 0 | P1 | TEE-S1 | 0.007096 | 0.001137 |
| 1 | P2 | TEE-S2 | -0.033184 | -0.010723 |
| 2 | P2 | RED-S1 | 0.021767 | 0.007034 |
| 3 | P3 | TEE-S3 | -0.051819 | -0.011879 |
| 4 | P3 | RED-S2 | 0.014382 | 0.003297 |
| 5 | P4 | RED-S3 | 0.011511 | 0.002094 |
| 6 | P4 | ELBOW-S4 | 0.084951 | 0.015452 |
| 7 | P5 | TEE-S1 | 16.014638 | 1.242356 |
| 8 | P5 | TEE-R1 | -0.200008 | -0.015516 |
| 9 | P5 | BAL-VLV-P5 | 34.754698 | 2.696141 |
| 10 | P5 | CTRL-VLV-P5 | 384.234911 | 29.807522 |
| 11 | P6 | TEE-S2 | 3.702657 | 0.620693 |
| 12 | P6 | TEE-R2 | 1.553274 | 0.260382 |
| 13 | P6 | BAL-VLV-P6 | 8.945757 | 1.499619 |
| 14 | P6 | CTRL-VLV-P6 | 100.019500 | 16.766731 |
| 15 | P7 | TEE-S3 | 4.149576 | 0.429221 |
| 16 | P7 | TEE-R3 | 1.525946 | 0.157840 |
| 17 | P7 | BAL-VLV-P7 | 19.485368 | 2.015514 |
| 18 | P7 | CTRL-VLV-P7 | 264.243001 | 27.332587 |
| 19 | P8 | BAL-VLV-P8 | 19.485368 | 3.544295 |
| 20 | P8 | CTRL-VLV-P8 | 104.878047 | 19.076814 |
| 21 | P9 | ELBOW-R4 | 0.084951 | 0.015452 |
| 22 | P10 | TEE-R3 | 0.481536 | 0.110387 |
| 23 | P10 | ENL-R3 | 0.032880 | 0.007537 |
| 24 | P11 | TEE-R2 | 0.502002 | 0.162221 |
| 25 | P11 | ENL-R2 | 0.041081 | 0.013275 |
| 26 | P12 | TEE-R1 | 0.188702 | 0.030234 |
| 27 | P12 | ENL-R1 | 0.073994 | 0.011855 |
Flow Paths#
ja.display_table(pipe_network.get_flow_path_table())
| path | Δp-elev. [kPa] | Δp-dyn. [kPa] | Δp-tot. [kPa] | Δp-deficit [kPa] | |
|---|---|---|---|---|---|
| 0 | P1|P2|P3|P4|P8|P9|P10|P11|P12 | 0.0 | 33.555200 | 33.555200 | 5.441810 |
| 1 | P1|P5|P12 | 0.0 | 38.997010 | 38.997010 | 0.000000 |
| 2 | P1|P2|P6|P11|P12 | 0.0 | 26.847643 | 26.847643 | 12.149367 |
| 3 | P1|P2|P3|P7|P10|P11|P12 | 0.0 | 36.290501 | 36.290501 | 2.706509 |
Statically Balance the Network for Design Volume Flow Rates#
To let the program balance the flow paths, simply call:
pipe_network.balance_network_at_design()
Now, we can check the required Kvr-settings of the balancing valves:
ja.display_table(pipe_network.get_balancing_valve_table())
| pipe ID | valve ID | Kvs | Kvr | |
|---|---|---|---|---|
| 0 | P5 | BAL-VLV-P5 | 1.33 | 1.330000 |
| 1 | P6 | BAL-VLV-P6 | 5.35 | 1.773348 |
| 2 | P7 | BAL-VLV-P7 | 2.32 | 1.515713 |
| 3 | P8 | BAL-VLV-P8 | 2.32 | 1.457026 |
Pipes, Fittings and Flow Paths Overview (ter)#
Pipes#
ja.display_table(pipe_network.get_pipe_table())
| pipe ID | L [m] | DN [mm] | Di [mm] | V [l/s] | v [m/s] | zeta | Re | Δp-dyn. [kPa] | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | P1 | 4.0 | 35.0 | 32.0 | 0.458 | 0.569476 | 0.007096 | 32945.645835 | 0.463923 |
| 1 | P2 | 2.0 | 28.0 | 25.0 | 0.397 | 0.808762 | -0.011416 | 36553.841457 | 0.580797 |
| 2 | P3 | 2.0 | 22.0 | 20.0 | 0.214 | 0.681183 | -0.037437 | 24630.107279 | 0.559724 |
| 3 | P4 | 2.0 | 18.0 | 16.0 | 0.122 | 0.606778 | 0.096462 | 17551.828785 | 0.629676 |
| 4 | P5 | 25.0 | 18.0 | 14.0 | 0.061 | 0.396263 | 434.804239 | 10029.616449 | 38.028212 |
| 5 | P6 | 25.0 | 26.0 | 20.0 | 0.183 | 0.582507 | 186.696474 | 21062.194542 | 36.687432 |
| 6 | P7 | 15.0 | 20.0 | 16.0 | 0.092 | 0.457570 | 315.569585 | 13235.805313 | 35.441478 |
| 7 | P8 | 20.0 | 20.0 | 16.0 | 0.122 | 0.606778 | 154.280699 | 17551.828785 | 34.184220 |
| 8 | P9 | 2.0 | 18.0 | 16.0 | 0.122 | 0.606778 | 0.084951 | 17551.828785 | 0.627582 |
| 9 | P10 | 2.0 | 22.0 | 20.0 | 0.214 | 0.681183 | 0.514415 | 24630.107279 | 0.686230 |
| 10 | P11 | 2.0 | 28.0 | 25.0 | 0.397 | 0.808762 | 0.543084 | 36553.841457 | 0.759983 |
| 11 | P12 | 4.0 | 35.0 | 32.0 | 0.458 | 0.569476 | 0.262696 | 32945.645835 | 0.504875 |
Fittings and Valves#
ja.display_table(pipe_network.get_fitting_table())
| conduit ID | fitting ID | zeta | pressure drop [kPa] | |
|---|---|---|---|---|
| 0 | P1 | TEE-S1 | 0.007096 | 0.001137 |
| 1 | P2 | TEE-S2 | -0.033184 | -0.010723 |
| 2 | P2 | RED-S1 | 0.021767 | 0.007034 |
| 3 | P3 | TEE-S3 | -0.051819 | -0.011879 |
| 4 | P3 | RED-S2 | 0.014382 | 0.003297 |
| 5 | P4 | RED-S3 | 0.011511 | 0.002094 |
| 6 | P4 | ELBOW-S4 | 0.084951 | 0.015452 |
| 7 | P5 | TEE-S1 | 16.014638 | 1.242356 |
| 8 | P5 | TEE-R1 | -0.200008 | -0.015516 |
| 9 | P5 | BAL-VLV-P5 | 34.754698 | 2.696141 |
| 10 | P5 | CTRL-VLV-P5 | 384.234911 | 29.807522 |
| 11 | P6 | TEE-S2 | 3.702657 | 0.620693 |
| 12 | P6 | TEE-R2 | 1.553274 | 0.260382 |
| 13 | P6 | BAL-VLV-P6 | 81.421043 | 13.648986 |
| 14 | P6 | CTRL-VLV-P6 | 100.019500 | 16.766731 |
| 15 | P7 | TEE-S3 | 4.149576 | 0.429221 |
| 16 | P7 | TEE-R3 | 1.525946 | 0.157840 |
| 17 | P7 | BAL-VLV-P7 | 45.651062 | 4.722023 |
| 18 | P7 | CTRL-VLV-P7 | 264.243001 | 27.332587 |
| 19 | P8 | BAL-VLV-P8 | 49.402652 | 8.986105 |
| 20 | P8 | CTRL-VLV-P8 | 104.878047 | 19.076814 |
| 21 | P9 | ELBOW-R4 | 0.084951 | 0.015452 |
| 22 | P10 | TEE-R3 | 0.481536 | 0.110387 |
| 23 | P10 | ENL-R3 | 0.032880 | 0.007537 |
| 24 | P11 | TEE-R2 | 0.502002 | 0.162221 |
| 25 | P11 | ENL-R2 | 0.041081 | 0.013275 |
| 26 | P12 | TEE-R1 | 0.188702 | 0.030234 |
| 27 | P12 | ENL-R1 | 0.073994 | 0.011855 |
Flow Paths#
ja.display_table(pipe_network.get_flow_path_table())
| path | Δp-elev. [kPa] | Δp-dyn. [kPa] | Δp-tot. [kPa] | Δp-deficit [kPa] | |
|---|---|---|---|---|---|
| 0 | P1|P2|P3|P4|P8|P9|P10|P11|P12 | 0.0 | 38.99701 | 38.99701 | 0.000000e+00 |
| 1 | P1|P5|P12 | 0.0 | 38.99701 | 38.99701 | 7.275958e-15 |
| 2 | P1|P2|P6|P11|P12 | 0.0 | 38.99701 | 38.99701 | 7.275958e-15 |
| 3 | P1|P2|P3|P7|P10|P11|P12 | 0.0 | 38.99701 | 38.99701 | 1.455192e-14 |
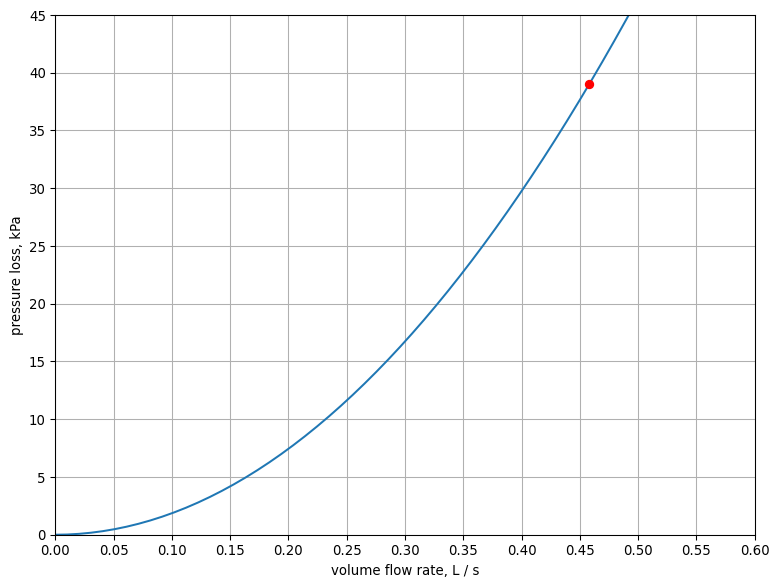
Drawing the System Curve of the Network#
Between the start and the end node of the balanced pipe network the pressure difference will be equal to the pressure loss along the critical path. As the network is balanced, each flow path between the start and the end node of the network creates the same pressure loss, as can be seen in the flow path table above. The ratio of the pressure difference to the square of the volume flow rate that enters the network through the start node (and leaves through the end node) is a measure of the hydraulic resistance of the balanced network. If the volume flow rate into the network at the start node of the network changes, the hydraulic resistance of the network remains the same, and as such the pressure difference between the start node and the end node of the network will change accordingly to the square of the volume flow rate. This relationship between the volume flow rate into (and out of) the network and the pressure difference across the hydraulic resistance of the pipe network is graphically presented by the system curve. However, if a control valve in the network changes its opening, the hydraulic resistance of the network will change, and as such the system curve will also change accordingly. Also, the network won’t be (perfectly) balanced anymore, meaning that volume flow rates through other cross-overs will also inevitably change. This will be demonstrated in a subsequent notebook.
from hvac.fluid_flow.utils import SystemCurve
system_curve = SystemCurve.create(pipe_network.hydraulic_resistance)
diagram = system_curve.diagram(
V_ini=Q_(0.0, 'L / s'),
V_fin=Q_(0.5, 'L / s'),
V_design=pipe_network.volume_flow_rate,
no_points=50,
fig_size=(8, 6),
dpi=96,
V_step=Q_(0.05, 'L / s'),
V_max=Q_(0.65, 'L / s'),
dP_step=Q_(5.0, 'kPa'),
dP_max=Q_(50.0, 'kPa'),
V_unit='L / s',
dP_unit='kPa'
)
diagram.show()
Save the Pipe Network for Later#
We will use this hydronic pipe network again in a subsequent notebook in which we will analyze the effect of closing control valves on the volume flow rates in the pipe network. Therefore, we save this pipe network on disk.
from hvac.fluid_flow.network import save_network
save_network(pipe_network, "./networks/hydronic_network.pickle")

